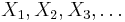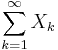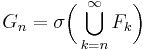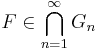Kolmogorov's zero-one law

In probability theory, Kolmogorov's zero-one law, named in honor of Andrey Nikolaevich Kolmogorov, specifies that a certain type of event, called a tail event, will either almost surely happen or almost surely not happen; that is, the probability of such an event occurring is zero or one.

Tail events are defined in terms of infinite sequences of random variables. Suppose

$X_1,X_2,X_3,\dots\,$

is an infinite sequence of independent random variables (not necessarily identically distributed). Then, a tail event is an event whose occurrence or failure is determined by the values of these random variables but which is probabilistically independent of each finite subset of these random variables. For example, the event that the series

$\sum_{k=1}^{\infty} X_k$

converges, is a tail event. The event that the sum to which it converges is more than 1 is not a tail event, since, for example, it is not independent of the value of X₁. In an infinite sequence of coin-tosses, a sequence of 100 consecutive heads occurring infinitely many times is a tail event.

In many situations, it can be easy to apply Kolmogorov's zero-one law to show that some event has probability 0 or 1, but surprisingly hard to determine which of these two extreme values is the correct one.

1 Formulation
2 See also
3 References
4 External links

Formulation

A more general statement of Kolmogorov's zero-one law holds for sequences of independent σ-algebras. Let (Ω,F,P) be a probability space and let F_n be a sequence of mutually independent σ-algebras contained in F. Let

$G_n=\sigma\bigg(\bigcup_{k=n}^\infty F_k\bigg)$

be the smallest σ-algebra containing F_n, F_n+1, …. Then Kolmogorov's zero-one law asserts that for any event

$F\in \bigcap_{n=1}^\infty G_n$

one has either P(F) = 0 or 1.

The statement of the law in terms of random variables is obtained from the latter by taking each F_n to be the σ-algebra generated by the random variable X_n. A tail event is then by definition an event which is measurable with respect to the σ-algebra generated by all X_n, but which is independent of any finite number of X_n. That is, a tail event is precisely an element of the intersection 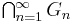$\textstyle{\bigcap_{n=1}^\infty G_n}$ .

References

Stroock, Daniel (1999), Probability theory: An analytic view (revised ed.), Cambridge University Press, ISBN 978-0-521-66349-6 .
Brzezniak, Zdzislaw; Tomasz Zastawniak (2000), Basic Stochastic Processes, Springer, ISBN 3-5407-6175-6
Rosenthal, Jeffrey S. (2006), A first look at rigorous probability theory, Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd., p. 37, ISBN 9789812703712

External links

The Legacy of Andrei Nikolaevich Kolmogorov Curriculum Vitae and Biography. Kolmogorov School. Ph.D. students and descendants of A.N. Kolmogorov. A.N. Kolmogorov works, books, papers, articles. Photographs and Portraits of A.N. Kolmogorov.

Kolmogorov's zero-one law

Contents

Formulation

See also

References

External links